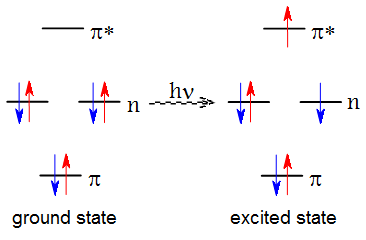
Most molecules have bound higher energy excited electronic states in addition to the ground electronic state E0. These states may be thought of as arising from the promotion of one of the electrons from the occupied orbital in the ground state to a vacant higher energy orbital. The excitation of an electron from the occupied orbital to a higher-energy orbital occurs when a photon with the energy that matches the difference between the two states interacts with the molecule. The classical Franck-Condon principle states that because the rearrangement of electrons is much faster than the motion of nuclei, the nuclear configuration does not change significantly during the energy absorption process. Thus, the absorption spectrum of molecules is characterized by the vertical excitation energies.
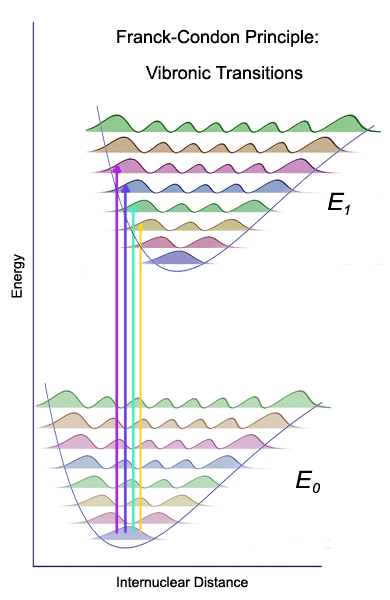The ground state (E0) supports a large number of vibrational energy levels. At room temperature, only the lowest vibrational level is populated, and electronic transitions originate from the n=0 vibrational level. The bound excited states (E1) also support several vibrational levels. However, because the excited state potential energy curve is typically shifted, the vertical excitations from the lowest vibrational level of the ground electronic state take the system into one of several vibrational levels of the excited electronic state. Thus, valence transitions, such as n → π* in carbonyl compounds show vibrational fine structure which may be useful for the characterization of the excited state. The quantum mechanical Franck-Condon principle states that the probability of each transition is determined by the extent of overlap between the ground state and excited state vibrational wave functions. These individual vibronic bands can be sometimes observed in the gas phase absorption spectra of molecules but the assignment of vibronic bands to specific states can be challenging. For example, if the two potential energy curves are significantly shifted, the 0 ← 0 transition may have so low intensity that it can escape detection. The spectra of molecules in solvents that interact strongly with the chromophore are broad and often featureless.
The absorption bands are typically classified as valence bands (for example, the local π → π* transition in many unsaturated organic molecules), Rydberg bands (transitions to very diffuse orbitals around the molecule), and charge transfer bands (involving electron transfer from one part of the molecule to another part). The lower energy bands typically arise from transitions from occupied valence orbitals to unoccupied valence orbitals. Many far-ultraviolet bands (below 200 nm) arise from Rydberg transitions. These bands can be recognized by the lack of vibrational fine structure and by the convergence of their energies toward the ionization potential of the molecule. The lowest energy transition in molecules that contain both lone pairs and π bonds is typically the n → π* transition. However, in some symmetric molecules, the intensity of the n → π* transition is very low because the transition is symmetry forbidden.
Excited states have limited life times (typically in the order of a nanosecond) and they can decay via several modes. Sometimes the excited state is so weakly bound that it will dissociate. For example, ozone undergoes a photodissociation to O2 and atomic oxygen after absorbing a photon of ultraviolet light. A second possibility is that the excited state returns to the ground state without emitting a photon. Such radiationless decay occurs readily when the excited state and the ground state potential energy curves meet via a conical intersection. For example, the excited states of DNA bases in Watson-Crick base paired geometry are very short-lived thanks to efficient radiationless decay; this protects DNA from photochemical damage. The third possibility of return to the ground state is via the emission of photon. Such radiative decay is commonly called fluorescence.
It is usually observed that the fluorescent light from molecules or nanoparticles has a longer wavelength than the exciting light. This immediately suggests that the emission of a photon from the electronically excited state is not a perfect mirror process of the absorption. Instead, the excited vibronic state rapidly relaxes on the excited state potential energy surface: the nuclei adopt a new optimum geometry that is at equilibrium with the excited state electronic wavefunction. In simple words, fluorescence usually takes place from the ground vibrational level of the electronically excited state E1. Again, because the rearrangement of electrons is very fast, the emission is vertical and reaches one of the vibrational levels of the ground electronic state E0. The energy difference between the relaxed excited state energy and the ground state energy is called the adiabatic excitation energy. Adiabatic excitation energies can be measured from the emission spectra of molecules.
Fluorescence occurs very quickly after excitation. There is another radative decay mode, called phosphoresence, which takes the system back to ground state over much longer timescales. In the case of phosphoresence, the excited state undergoes a change in the spin state. In a typical scenario, the potential energy surface of a singlet excited state crosses with the potential energy surface of a lower-laying triplet energy state, and the system becomes trapped in the triplet excited state. Spontaneous emission from triplet excited state to singlet ground state is spin forbidden, and thus occurs with a low probability. The phenomena of fluorescence and phosphoresence are two manifestations of luminescent emission.
Computational methods could, in principle give accurate information about the excited electronic states. For example, the vertical excitation energy can be obtained in the first approximation as the energy difference between the excited state potential energy curve and the ground state potential energy curve at the ground state minimum energy geometry. Optimization of geometry of the excited electronic state allows to calculate adiabatic excitation energies. Thus, computations could be used to predict absorption and fluorescence emission spectra of molecules. With a little more effort, the absorption of chiral light can be characterized, allowing one to predict the circular dichroism spectra. Such calculations are often valuable for chemists interested in the identification of molecules solely on the basis of their spectra.
A large number of computational methods have been developed for the description of excited states. On one hand, we have easy-to-apply methods, such as Configuration Interaction Singles (CIS) or Time Dependent Density Functional Theory (TDDFT) but these have a generally limited accuracy, and can fail spectacularly for certain situations. On the other hand, multireference configuration interaction methods typically offer an accuracy of about 0.1 eV (2.3 kcal/mol) but require expertise in setting up the calculation. In general, meaningful excited state calculations can be difficult to carry out. There are special cases where a simple method like (CIS) will give useful answers. In general, however, one must be aware of pitfalls such as: