
Molecular recognition involves specific interaction between molecules that lead to the formation of thermodynamically stable, relatively long-lived complexes. These specific interactions include:
Many of the forces that drive molecular recognition are short-range; strong interactions is achieved only if the molecular surfaces of interacting moieties can be close to each other. Few of the forces, such as the Coulombic attraction between unlike charges are rather long range, but in the aqueous solution water between interacting charges strongly attenuates the interaction. In summary, tight binding is achieved when the shape and the charge distribution of the receptor cavity is optimally matched by the shape and the charge distribution of the ligand molecule.
In order to rationally design molecules with a good shape complementarity, the question of what determines a shape of the molecular surface must be considered. The shape of a molecule is determined by the electron density of the molecule because the Pauli exclusion principle prohibits the the intrusion of a second molecule into the region where a pair of electrons from the first molecule already resides. However, the quantum mechanics is a probabilistic theory and there is no sharp boundary between a region that the second molecule is prohibited from entering, and the rest of the space. Instead, the electron density falls off roughly exponentially with the distance from the nucleus, and the repulsive energy grows roughly exponentially as the distance between two nuclei decreases. In typical molecules, the increase is so rapid that one molecule cannot penetrate into a region just about half an angstrom beyond the point of minimum interaction. The electron density depends on the atomic composition and the chemical connectivity of atoms in the molecule. One way to determine molecular shape is to calculate the electron density, and display the region where the electron density is larger than some cut-off value as a three-dimensional surface. Such calculations necessitate a quantum chemical approach and are possible with most drug-like organic molecules. For larger molecules, such as proteins, Connolly surfaces and solvent-accessible surfaces can be calculated rapidly based on empirical van der Waals radii of atoms.

Electrostatic potential surfaces are valuable in computer-aided drug design because they help in optimization of electrostatic interactions between the protein and the ligand. These surfaces can be used to compare different inhibitors with substrates or transition states of the reaction. Electrostatic potential surfaces can be either displayed as isocontour surfaces or mapped onto the molecular electron density. The latter are more widely used because they retain the sense of underlying chemical structure better than isocontour plots.
Many molecular visualization programs allows display of electrostatic potential maps based on quantum chemical calculations. MOLDEN is able to calculate electron density surfaces and electrostatic potential surfaces based on the information in the output files of Gaussian or Firefly (PC GAMESS) calculations. MOLDEN offers three ways to evaluate the electrostatic potential. First, it can calculate the true electrostatic potential based on molecular orbital data. This is rather time consuming, especially if large Gaussian basis sets were used to form molecular orbitals, but should give the best representation of the electrostatic potential. Second, MOLDEN can perform fitting of the electrostatic potential based on the quantum-chemically derived multipole moments of the molecule. In other words, it tries to guess what kind of potential would best reproduce the dipole and octupole moment of the molecule. Third, MOLDEN can calculate the electrostatic potential based on partial atomic charges. This is the fastest but least reliable method because atomic charges themselves may be unreliable, or simply do not capture properly the electronic structure of the molecule. For example, six slightly negative charges on carbons balanced by six slightly positive charges on hydrogens do a poor job capturing the essence of the negatively charged π cloud above and below the six-membered ring. The image below illustrates electrostatic potential maps for benzene using the true potential, multipole-derived, and charges-based methods.
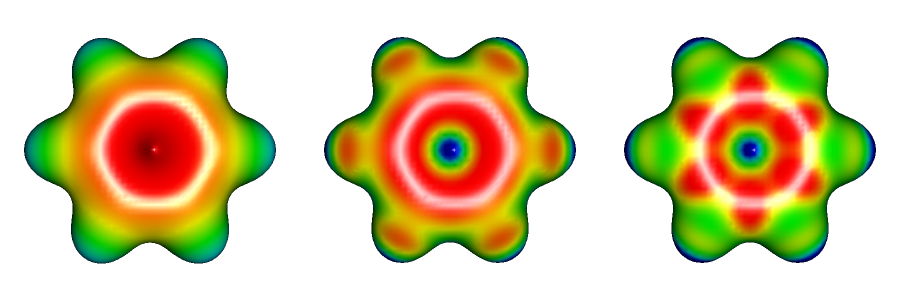
The electron density surface onto which the potential is mapped can be calculated at different density levels. The suggested value in MOLDEN, 0.02 is appropriate for the analysis of non-covalent interactions as it roughly corresponds to the surface that two non-reacting molecules can approach. Larger values, e.g. 0.05 may be useful if one is interested in how the electron distribution within the molecule determines its reactivity. The image below shows the electrostatic potentials of benzene with true potential, multipole-derived, and charges-based methods using the cutoff value of 0.05.
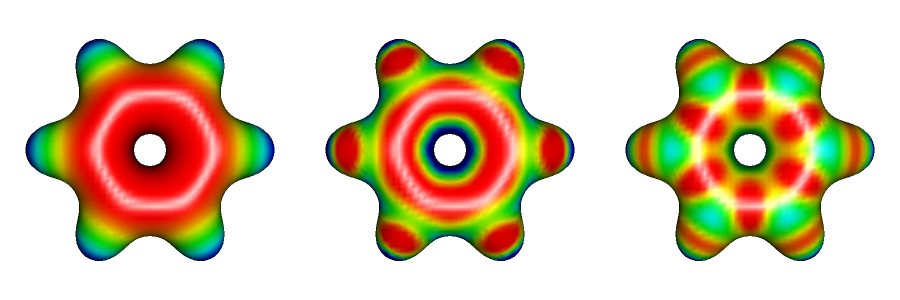
Benzene is a typical apolar molecule and its electrostatic potential map just emphasizes that there is a significant electron density, and negative potential above and below the aromatic ring. The true potential correctly captures the delocalized nature of this electron density while charges-based method incorrectly suggest that the negative potential is less pronounced at the position of carbon atoms. The latter notion is in disagreement with the chemical reactivity of benzene: it readily undergoes electrophilic substitutions but is inert toward nucleophiles. All maps correctly suggest that hydrogens in the benzene are only slightly positively charged. Also notice that both the multipole-derived, and charges-based method incorrectly predict that the very centre of the benzene ring has a large positive potential. Only the true electrostatic potential would lead to the firm conclusion that the π face or benzene would bind cations well. One could also predict the existence of a T-shaped benzene dimer in which a slightly positively charged hydrogen from one molecule points toward the centre of the aromatic ring of the other molecule.
Electrostatic potential maps for polar molecules reveal well sites that are most electron-rich and most electron-poor. Keep in mind that the maps represent the potential due to all electrons and thus an electron-poor site in the molecule is not necessarily the most electrophilic site. However, true electrostatic potential maps of polar molecules generally do an excellent job predicting the possibility of charge-dipole, dipole-dipole, and quadrupole-dipole interactions. As seen from the example below, the true electrostatic potential correctly suggest that the polar hydrogen in pyrrole can participate in hydrogen bonding. In contrast, the charge-based method gives a qualitatively incorrect description for pyrrole.
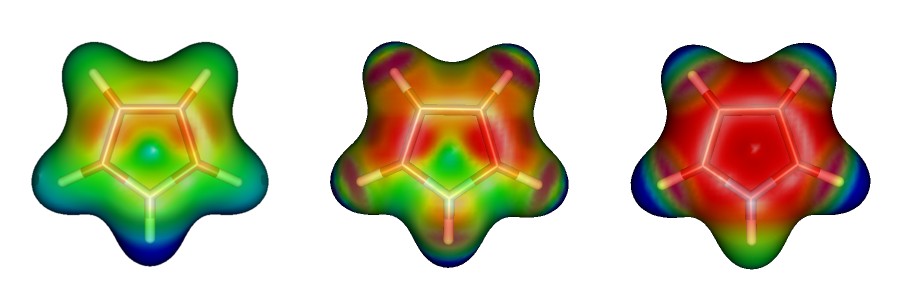
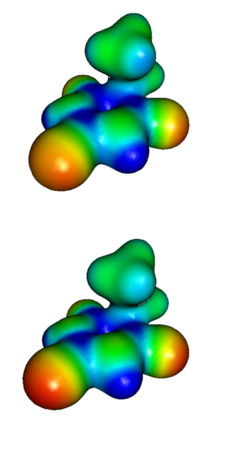 MOLDEN and other similar visualization programs calculate the true electrostatic potential based on quantum mechanically derived molecular orbitals. The quality of these orbitals thus determines the reliability of the true electrostatic potential. The quality of molecular orbitals, in turn depends on factors such as the number of Gaussian functions that are used to describe each atomic orbital, and the structure of the Hamiltonian (quantum-mechanical expression that gives molecular orbital energies). Fewer Gaussian functions make the calculation less accurate but much faster. Simplifying the Hamiltonian, e.g. by ignoring dynamic correlation between the motion of electrons also leads to loss of accuracy but allows analysis of larger molecules. Molecular electrostatic potentials are usually calculated using a simplified Hamiltonian that ignores electron correlation (the Hartree-Fock method) using a small or modest basis set (3-21G or 6-31+G(d,p)). The time of calculating molecular orbitals with Gaussian or Firefly (PC GAMESS), increases significantly when a larger basis is used; the time of evaluating true electrostatic potential with MOLDEN may easily reach hours with larger basis. It appears that for typical drug design tasks with stable molecules, 3-21G basis is sufficient. The image on the right compares true electrostatic potential maps of diethyl barbiturate with 3-21G and 6-31+G(d,p) bases.
MOLDEN and other similar visualization programs calculate the true electrostatic potential based on quantum mechanically derived molecular orbitals. The quality of these orbitals thus determines the reliability of the true electrostatic potential. The quality of molecular orbitals, in turn depends on factors such as the number of Gaussian functions that are used to describe each atomic orbital, and the structure of the Hamiltonian (quantum-mechanical expression that gives molecular orbital energies). Fewer Gaussian functions make the calculation less accurate but much faster. Simplifying the Hamiltonian, e.g. by ignoring dynamic correlation between the motion of electrons also leads to loss of accuracy but allows analysis of larger molecules. Molecular electrostatic potentials are usually calculated using a simplified Hamiltonian that ignores electron correlation (the Hartree-Fock method) using a small or modest basis set (3-21G or 6-31+G(d,p)). The time of calculating molecular orbitals with Gaussian or Firefly (PC GAMESS), increases significantly when a larger basis is used; the time of evaluating true electrostatic potential with MOLDEN may easily reach hours with larger basis. It appears that for typical drug design tasks with stable molecules, 3-21G basis is sufficient. The image on the right compares true electrostatic potential maps of diethyl barbiturate with 3-21G and 6-31+G(d,p) bases.
This tutorial illustrates how to use quantum chemistry calculations to generate and display molecular electron density surfaces and map electrostatic potential values to the surface. You will compare two conformers of oxamic acid. Oxamate, anion of oxamic acid is a powerful inhibitor for Plasmodium falciparum lactate dehydrogenase and thus may serve as a fragment or lead in developing novel anti-malaria drugs. The molecule has two low energy conformers that differ in the dihedral angle about the central C-C bond. These conformers are shown in the image on the right.
Your task is to calculate and display electrostatic potential of cis and trans oxamic acid. Molecular surfaces should be calculated based on optimized molecular geometries. While molecular mechanics force fields can be used to generate reasonable initial geometries, it is considered a good practice to optimize molecular geometries with quantum mechanical methods prior generation of electron molecular electrostatic potential surfaces. In this tutorial you start with previously optimized structures of cis and trans oxamic acid because optimization jobs can be time-consuming. The quantum chemistry program Gaussian was used to perform geometry optimization for the two conformers. The calculation was performed at the Moller-Plesset second order perturbation theory level with a moderate-sized basis set to describe molecular orbitals. Specifically, a 6-311+G(d,p) basis set was used which allows for some polarization of electron density on both heavy atoms and hydrogens. In computational jargon, the molecule was optimized at the MP2/6-311+G** level. The comparison of relative energies of the two conformers suggests that s-trans conformer is more stable by 1.68 kcal/mol. You can use MOLDEN to launch quantum mechanical geometry optimizations but keep in mind that optimizing a larger molecule using accurate QM methods can be very time-consuming.