The general Schrodinger equation for any molecule depends on electronic coordinates (r) and on nuclear coordinates (R):
This equation can be solved analytically only for two interacting particles, e.g. for hydrogen atom. Solutions for other systems require further approximations. One commonly made approximation in the quantum mechanical description of molecules is the Born-Oppenheimer approximation, which separates the motion of electrons from the motion of nuclei. The mathematical derivation of the Born-Oppenheimer approximation is not considered here, but the approximation is based on the ansatz (educated guess) that the total wave function of the molecule is a product of electronic and nuclear wave functions. Similarly, the total molecular Hamiltonian is taken to separable into electronic and nuclear Hamiltonians.
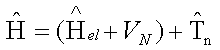
Effectively, the molecular Schrodinger equation is decomposed into the electronic Schrodinger equation, and the nuclear Schrodinger equation. So far, we have been concerned with the solution to the electronic Schrodinger equation for a given nuclear configuration:
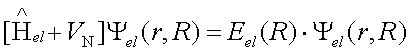
The solution to the electronic Schrodinger equation gives the electronic energy that also includes the constant nuclear repulsion term. Minimization of the electronic energy by varying the molecular geometry gives the minimized molecular structure. The electronic energy acts as a potential that confines nuclei into a low energy geometry that we call the molecule. At the beginning of this course you minimized systems that were described by the classical quadratic or Morse potentials, and found the distances at which the potential was minimal. In quantum mechanical description of molecules, we have a more complex potential but the principles of geometry optimization are the same as in classical mechanics. However, the motions of nuclei on the potential energy surface around the minimum is not correctly described by classical mechanics. To describe the vibration of atoms in the molecule or crystal, quantum mechanics is needed.
Description of nuclear motions in quantum mechanics requires solving the nuclear Schrodinger equation. The solution to this equation will give the allowed energy levels En and wave functions &Psin for each of the energy level. In general, we do not know what these wave functions are but it will be shown later that the vibrational wave functions in the quadratic potential are the Hermite polynomials. Perturbation theory or variational calculations can be used to obtain wave functions for more realistic potentials. The square of the wave function gives the probability distribution for the interatomic distance. Knowledge of vibrational energy levels allows one to calculate the position of vibrational (infrared) spectral lines. Knowledge of vibrational wave functions allows to calculate the intensity of vibrational spectral lines. Analysis of vibrational wave functions of molecules in ground electronic state and electronically excited state allows to predict optical properties of molecules and materials. Practical applications include design of novel dyes, organic semiconductors, and photonic devices,
The nuclear Hamiltonian contains the kinetic energy operator and the potential energy operator. The kinetic energy operator is obtained from a relationship T = p2/(2 μ) and the potential energy operator for nuclear motion is the electronic energy:
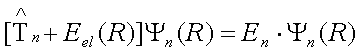
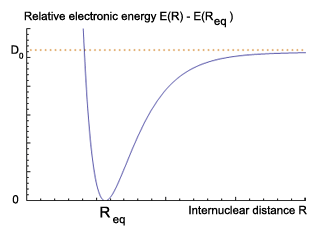In practice, we are interested of nuclear motions about the minimum energy structure and we can subtract the electronic energy of the minimum energy configuration from the electronic energy at every other point to get the nuclear Schrodinger equation in relative energy. Solving the nuclear Schrodinger equation below is difficult because of the complex nature of the potential energy operator. However, approximate solution near the minimum energy geometry can be readily derived assuming that the potential is quadratic in this region.
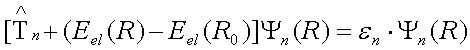
System confined by quadratic potential is known to undergo harmonic oscillations about the equilibrium position. You are probably familiar with the classical harmonic oscillator because of the importance of this model in physics. An example of classical harmonic oscillator is a system consisting of two masses (m1 and m2 that are connected by an ideal spring and do not experience any frictional forces. Recall that such system undergoes harmonic oscillation with frequency that depends on the force constant (oscillators with stiff bonds have high frequencies) and the reduced mass (oscillators with larger reduced masses vibrate at lower frequencies).
Harmonic oscillator is one of the few systems for which analytical solution to Schrodinger equation is possible. An example solution using Mathematica is illustrated here. It is important to recognize that the force constant enters the nuclear Schrodinger equation as an input parameter, and the solution to the Schrodinger equation consists of allowed energy levels and corresponding wave functions. The energy difference between harmonic oscillator energy levels is constant. In the quantum mechanical picture, absorption of photon can occur if the energy of photon matches the energy gap between two states. Selection rules dictate that only transitions that change the vibrational quantum number by one are allowed; thus a single frequency is absorbed by harmonic oscillator.
The light absorption by diatomic molecule can be also understood from the classical model of vibrating molecule. In the classical picture, the molecule does not have discrete energy levels but can gain energy from the oscillating electromagnetic field only when the frequency of the field matches the characteristic frequency of the vibration. Furthermore, efficient energy transfer requires that the dipole moment of the molecule must change during vibration. It turns out that the mechanical frequency of the classical harmonic oscillator is equal to the quantum mechanical prediction for frequency that satisfies the Bohr frequency condition ΔE = hν
We can now see the distinction between the classical and quantum mechanical description of nuclear motions. In classical mechanics, motion of nuclei is entirely thermal: at 0 K the system is confined to the minimum energy geometry, and at higher temperatures the system explores higher energy regions with Boltzmann probability. Classical Monte Carlo simulations could be used to characterize the range of nuclear motions and calculate average energy of the vibrating molecular system. One of the general principles of quantum mechanics is that a system that is confined by a potential can only exists at certain discrete energy values. Atoms undergo vibtaions even at absolute zero, and the vibrational energy of the system should be calculated from the partition function that ioncludes all vibrational states. In case of harmonic potential this sum converges because higher energy states contribute less and less to the sum.