The problem of estimating Pi from the areas of the circle and the square can be cast in the form of integral evaluations. Recall that according to geometric interpretation, integral is the area under the curve or the area enclosed by a shape. The ratio of the area of a circle to the area of a square is given by the following ratio of integrals:
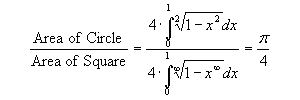Thus, the Monte Carlo method can be used to numerically evaluate various integrals. Of course, integrals can be numerically evaluated by many methods, such as by the trapezoidal rule or the Simpson's rule. While such numerical schemes are effective in evaluating one-dimensional integrals, they became more time-consuming, and eventually intractable as the dimensionality of the integral grows. The inability to evaluate multidimensional integrals by traditional methods is known as the "Curse of Dimensionality". Monte Carlo integration does not suffer from the Curse of Dimensionality and becomes more and more competitive over other numeric integration technique as the dimensionality of the integral grows.
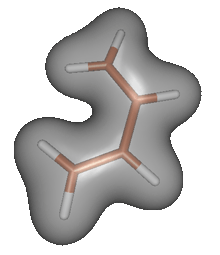Multidimensional integrals are common in chemistry. A simple example is the estimation of a volume of a molecule. In general, the volume of molecule is given by the following integral, which usually cannot be evaluated analytically.
Molecules of course do not have sharp boundaries, but we can define the volume of a molecule as the volume of a region where the electron density is larger than some cut-off value (e.g. 0.2 electrons per cubic angstrom). To determine the volume of a molecule by Monte Carlo integration, we can randomly sample points within a box that encloses the molecule; the volume of the molecule can be calculated from the ratio of points that fall within the region with electron density above the cut-off to the total number of points.
More complex multidimensional integrals are encountered in statistical thermodynamics of liquids and macromolecules. For example, the heat of vaporization of a liquid depends on the ways molecules interact with each other in the liquid. Because molecules in the liquid are constantly moving around, the strength of interactions of each molecule with its neighbors is changing at the microscopic level. We can simulate these changes in molecular configuration of a liquid using the Monte Carlo method. In this approach, some liquid molecules are randomly moved around to generate new configurations. Averaging over a sufficiently large number of molecular orientations allows to estimate average interaction strength, which is related to the heat of vaporization.
There is a serious practical problem with the above approach, however. Random moves of liquid molecules often result in molecules bumping into each other, so if we were to count every change, we will end up with a large number of configurations that are very high in energy. Boltzmann distribution dictates that configurations with high energy are improbable and do not contribute significantly to average properties. Specifically, an expectation value for a property, such as energy, of a system in thermal equilibrium is given in statistical thermodynamics by formula:
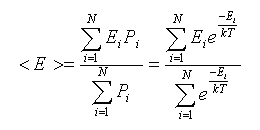The probabilities, Pi, play a role of weight factors in the sum in the numerator, and they become quickly very small as the energy of a configuration increases. In other word, purely random generation of configurations leaves us with very few "valuable" configurations and most of the computer time is wasted by generation of configurations that are improbable according to the Boltzmann distribution. How could we sample the system so that low energy states occur more frequently than high-energy states?